9713. Common Math Formulas
Math Formulas

Common math formulas.

1. Geometry

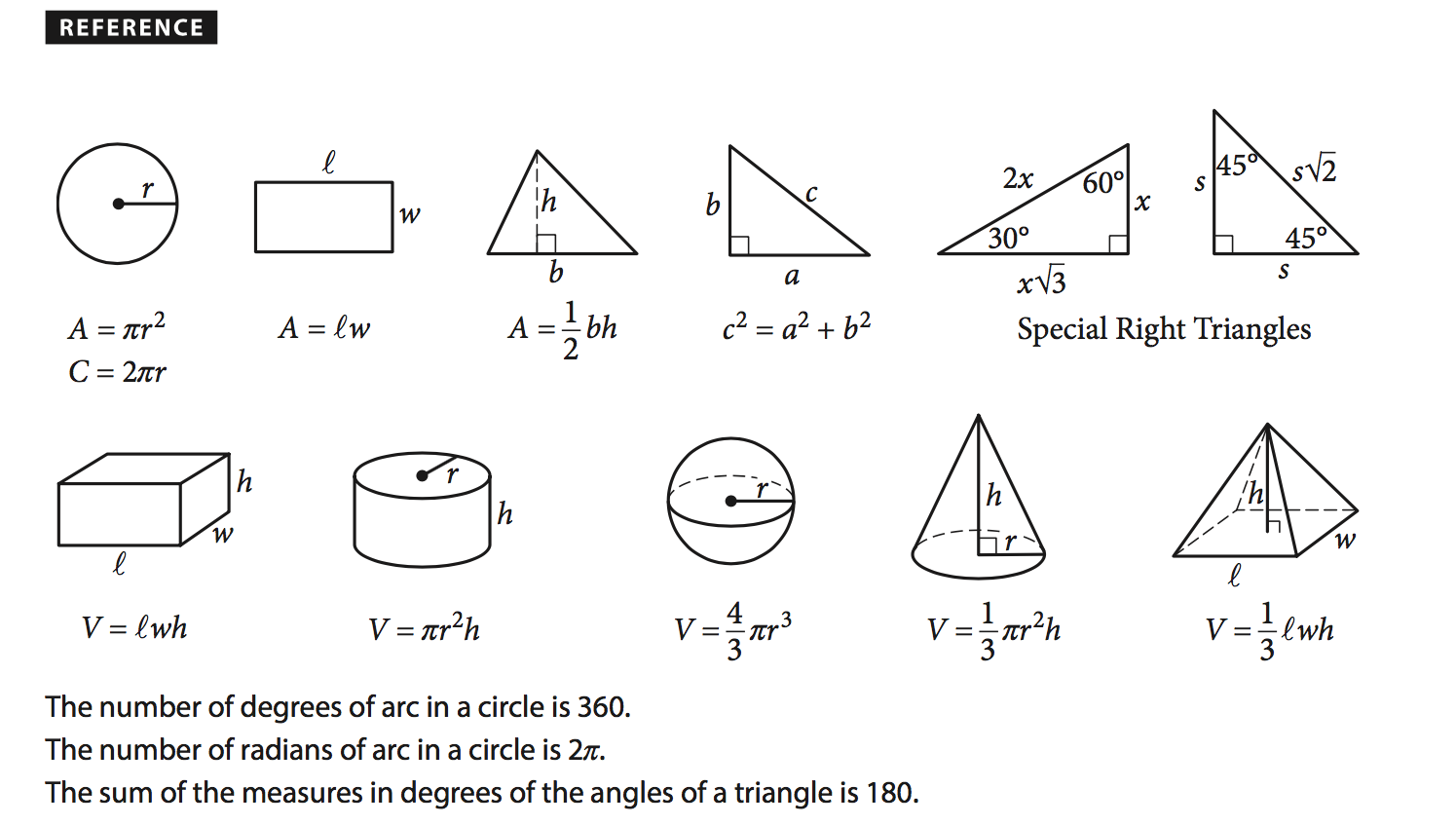
image

1.1 Perimeter

Shape Formula Explanation
Square $P = 4a$ where a = any edge
Rectangle $P = 2l + 2w$ where l = length and w = width
Triangle $P = a + b + c$ where a = side, b = base, and c = side
Circle $P = {\pi}d$ or $P = 2{\pi}r$ where $\pi$ = 3.14, d = diameter and r = radius

1.2 Area

Shape Formula Explanation
Square $A = a^2$ where a = any side of the square
Rectangle $A = lw$ where l = length and w = width
Parallelogram $A = bh$ where b = base and h = height
Triangle $A = \frac{1}{2}bh$ where b = base and h = height
Triangle $A = \vert \frac{(A_x(B_y-C_y) + B_x(C_y-A_y)+C_x(A_y-B_y)}{2}\vert$ where ($A_x$,$A_y$) are the x and y coordinates of the point A, etc.
Circle $A = \pi r^2$ where $\pi$ = 3.14 and r = radius
Trapezoid $A = \frac{a + b}{2}h$ where a = top base, b = bottom base, and h = height
Sphere $S = 4{\pi}r^2$ where S = surface area, $\pi$ = 3.14 and r = radius
Cube $S = 6a^2$ where a = any edge
Cylinder $S = 2{\pi}rh$ where $\pi$ = 3.14, r = radius, and h = height

1.3 Volume

Shape Formula Explanation
Cube $V = a^3$ where a = any edge
Rectangular Container $V = lwh$ where l = length, w = width, and h = height
Square Pyramid $V = \frac{1}{3}b^2h$ where b = base length, h = height
Cylinder $V = πr^2h$ where $\pi$ = 3.14, r = radius, and h = height
Cone $V = \frac{1}{3}\pi r^2h$ where $\pi$ = 3.14, r = radius, and h = height
Sphere $V = \frac{4}{3}\pi r^3$ where $\pi$ = 3.14, r = radius
Right Circular Cylinder $V = \pi r^2h$ where $\pi$ = 3.14, r = radius, and h = height

2. Trigonometry

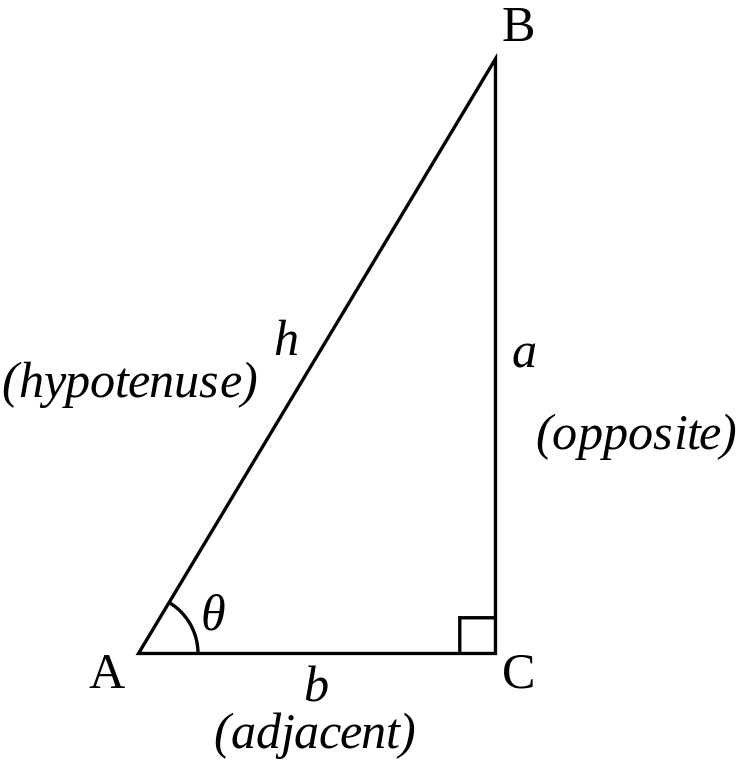
image

Function Formula
Sine $\sin\theta=\frac{opposite}{hypotenuse}$
Cosine $\cos\theta=\frac{adjacent}{hypotenuse}$
Tangent $\tan\theta=\frac{opposite}{adjacent}$, or $\tan\theta=\frac{\sin\theta}{\cos\theta}$
Cosecant $\csc\theta=\frac{1}{\sin\theta}$
Secant $\sec\theta=\frac{1}{\cos\theta}$
Cotangent $\cot\theta=\frac{1}{\tan\theta}$, or $\cot\theta=\frac{\cos\theta}{\sin\theta}$
Equation ${\sin}^2\theta+{\cos}^2\theta = 1$

3. Formulas/Equations

Title Formula Explanation
Distance between two points $d=\sqrt{(x_2-x_1)^2+{(y_2-y_1)^2}}$ where ($x_1$,$y_1$) and ($x_2$,$y_2$) are two points on a coordinate plane
Slope of a line $m=\frac{y_2-y_1}{x_2-x_1}$ where ($x_1$,$y_1$) and ($x_2$,$y_2$) are two points on a coordinate plane
Equation of a line $y=mx+b$ where m is the slope and b is the y-intercept
Quadratic Equation $ax^2+bx+c=0$ where a and b are coefficients and c is constant
Quadratic formula $x={-b\pm \sqrt{b^2-4ac}\over 2a}$ where a and b are coefficients and c is constant
Equation of a circle $(x-h)^2+(y-k)^2=r^2$ where r is the radius and (h, k) is the center
Logarithm Equation $\log_{b}x=y$, $b^y=x$  
Logarithm Equation $log_{b}xy=log_b{x}+log_{b}y$  
Logarithm Equation $log_{b}\frac{x}{y}=log_b{x}-log_{b}y$  

4. Algebraic Rules

Title Formula Explanation
Product Rule $ a^n \times a^m = a^{n+m}$ where a is the base, n and m are the exponents
Power Rule $ (a^n)^m = a^{nm}$ where a is the base, n and m are the exponents
Quotient Rule $ \frac{a^n}{a^m} = a^{n-m}$ where a is the base, n and m are the exponents
Negative Exponent $ a^{-n} = \frac{1}{a^n}$ where a is the base, n is the exponent

5. Formulas

5.1 Sum of Integers 1 through N

If

then reverse the series and rewrite that as

Adding the two together

or

5.2 Sum of Powers of 2

Proofs: Look at these values in binary way.

Power Binary Decimal
$2^0$ 000001 1
$2^1$ 000010 2
$2^2$ 000100 4
$2^3$ 001000 8
$2^4$ 010000 16
$2^5$ 100000 32

Example 1:

Example 2:

5.3 Permutation and Combination

Permutation:

Example: Choose 2 numbers from array [1,2,3,4], return the total number of all possible permutations.

Combination:

Example: Choose 2 numbers from array [1,2,3,4], return the total number of all possible combinations.

6. References